Для многих не секрет, что в играх часто используются карты созданные из так называемых тайлов (от англ. tile — плитка).

Более распространённое использование получили прямоугольные (квадратные) тайлы, т.к. они очень просты в ориентации и расчётах на них. Но так же они имеют ограничения и неудобные неточности, например: движение по диагонали не равно по расстоянию движению в стороны и, как следствие, движение зачастую ограничивается четырьмя направлениями.

Для решения таких проблем придумали использовать гексагональные тайлы. Поле с гексагональной разметкой обладает множеством преимуществ: гексагонами можно замостить бесконечную плоскость и расстояния до любого соседнего тайла равны между собой.

Но гексагональное поле привносит чуть более сложные расчёты для программиста, а так же я зачастую встречаю сложности представления двумерного массива в виде гексагонального поля и наоборот, т.к. ячейки располагаются не так просто как квадратные, а со смещением.

Поэтому в этой статье мы рассмотрим основы построения такого поля и начальные необходимые расчёты на нём, такие как определение клетки поля под курсором, её соседних клеток.

Виды гексагональных полей

На самом деле гексагональное поле определяется так же легко как прямоугольное поле. Вот наглядная демонстрация этой трансформации:

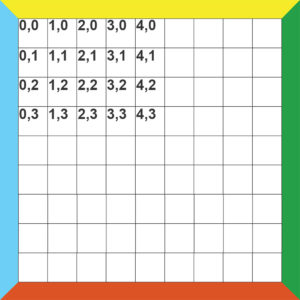
В клеточках написаны координаты клетки в двумерном массиве (x, y).

Хорошо видно, что поменялся лишь метод отображения путём смещения каждого чётного ряда вправо на половину длины гексагона. А массив клеток можно по прежнему держать в виде двумерного массива.

Мы можем располагать шестиугольники двумя способами, я назвал их «горизонтальное» и «вертикальное». На картинке выше мы видим «горизонтальное» расположение гексагонов. А вот вертикальное:

В вертикальном поле смещается не ряд, а столбец и шестиугольники ориентируются ребром вверх.

Ещё есть разновидность «горизонтального» поля с постоянным смещением ряда в одну сторону:

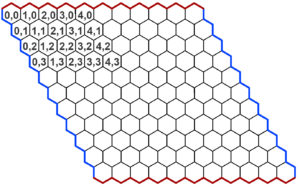
Построение поля

У всех видов полей будет одна математическая модель — двумерный массив, но будут отличаться алгоритмы отображения ячеек (это видно наглядно), распознавание ячейки по координатам и нахождение соседних ячеек.

Я не буду разбирать программное отображение полей (т.е. рисование ячеек программными методами) т.к. это примитивно и не интересно для практического геймдева. Я сразу возьму графические гексагональные тайлы как для реальной игры или прототипа таковой.

Для удобного индексирования разных видов тайлов нам понадобится небольшая база данных, оформим её в файле DB.ts, вот её код:

namespace DB {

  export const TILES = [
    {
      name: 'grass',
      tiles: ['grass_05', 'grass_10', 'grass_12', 'grass_14']
    },
    {
      name: 'dirt',
      tiles: ['dirt_06', 'dirt_12', 'dirt_14', 'dirt_18']
    },
    {
      name: 'sand',
      tiles: ['sand_07', 'sand_13', 'sand_14', 'sand_18']
    }
  ];

  export function getTileFrameName(tile_name_id: number, tile_id: number): string {
    return TILES[tile_name_id].tiles[tile_id];
  }

}

Здесь у нас массив видов земель и их тайлов и функция удобного извлечения имени тайла в атласе по id-шникам земли и тайла.

Массив для отображения нашей карты мы определим заранее, как если бы мы заранее создали карту для игры в самодельном редакторе карт. Определим его в файле класса состояния игры и вот как он выглядит:

const MAP = [
  [{ tid: 2 }, { tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 0 }],
  [{ tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 0 }, { tid: 0 }],
  [{ tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 1 }, { tid: 1 }],
  [{ tid: 0 }, { tid: 0 }, { tid: 1 }, { tid: 3 }, { tid: 2 }],
  [{ tid: 0 }, { tid: 0 }, { tid: 1 }, { tid: 2 }, { tid: 1 }]
];

Я постарался сделать лесок в левом верхнем углу и гору с лесом в правом нижнем углу.

Т.к. у нас тайлы ориентированы для горизонтального поля, то с него и начнём.

Горизонтальное поле

Для графического отображения нам нужно знать размер тайла по горизонтали и вертикали и начальную точку в которой будет располагаться самый первый (в нашем случае левый верхний) тайл. Эти параметры можно легко подобрать в ручную. Размеры тайла и координаты поля мы определим константами и вот как будет выглядеть функция построения:

Код построения горизонтального поля

module PhaserGame.Client {

  const MAP = [
    [{ tid: 2 }, { tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 0 }],
    [{ tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 0 }, { tid: 0 }],
    [{ tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 1 }, { tid: 1 }],
    [{ tid: 0 }, { tid: 0 }, { tid: 1 }, { tid: 3 }, { tid: 2 }],
    [{ tid: 0 }, { tid: 0 }, { tid: 1 }, { tid: 2 }, { tid: 1 }]
  ];

  const TILE_SIZE = { w: 120, h: 138 };
  const FIELD_POS = { x: 250, y: 100 };

  export class HexHorMenu extends Phaser.State {
    private mainDummy: Phaser.Sprite;
    private tnid = 0;

    private sectorWidth = TILE_SIZE.w;
    private sectorHeight = 3 / 4 * TILE_SIZE.h;

    private mapWidth = MAP[0].length;
    private mapHeight = MAP.length;

    create() {
      this.mainDummy = new Phaser.Sprite(this.game, 0, 0);
      this.add.existing(this.mainDummy);

      // random tile name id
      this.tnid = MyMath.randomIntInRange(0, 2);

      for (var j = 0; j < this.mapHeight; j++) {
        const row = MAP[j];
        for (let i = 0; i < row.length; i++) {
          const tid = row[i].tid;
          var tpos = this.getTilePosition(i, j);
          var tile = new Phaser.Sprite(this.game, tpos.x, tpos.y, 'game', DB.getTileFrameName(this.tnid, tid));
          tile.anchor.set(0.5);
          this.mainDummy.addChild(tile);
        }
      }
    }

    private getTilePosition(col_id: number, row_id: number): Phaser.Point {
      var res = new Phaser.Point(
        FIELD_POS.x + col_id * this.sectorWidth + (row_id % 2 > 0 ? this.sectorWidth / 2 : 0),
        FIELD_POS.y + row_id * this.sectorHeight
      );
      return res;
    }

  }

}

Размеры тайла я сначала указал равными размерам графики тайла (120 и 140), но при первом запуске оказалось, что получился небольшой зазор по вертикали, поэтому пришлось уменьшить высоту тайла на 2 (h = 138) пикселя и плитки легли плотно.

Line 18-19: определение размеров сектора тайла. Сектор — это прямоугольник из которых образуется неразрывная сетка поля, они наглядно отображены на следующем рисунке;

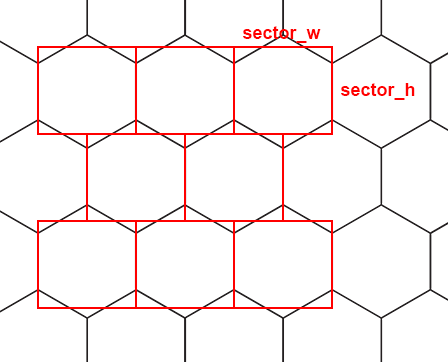
Как можно заметить, ширина сектора равна ширине тайла, а высота сектора = 3/4 высоты тайла.

Line 29: рандомно определяем id типа тайлов (трава, грязь или пустыня);

Line 31-40: цикл создания и расположения тайлов для отображения;

Line 32: получаем текущий ряд поля;

Line 34: получаем id текущего тайла из базы;

Line 45: рассчитываем x-координату текущего тайла со смещением каждого второго ряда на половину ширины сектора;

Line 46: рассчитываем y-координату тайла с отступом на высоту сектора вниз;

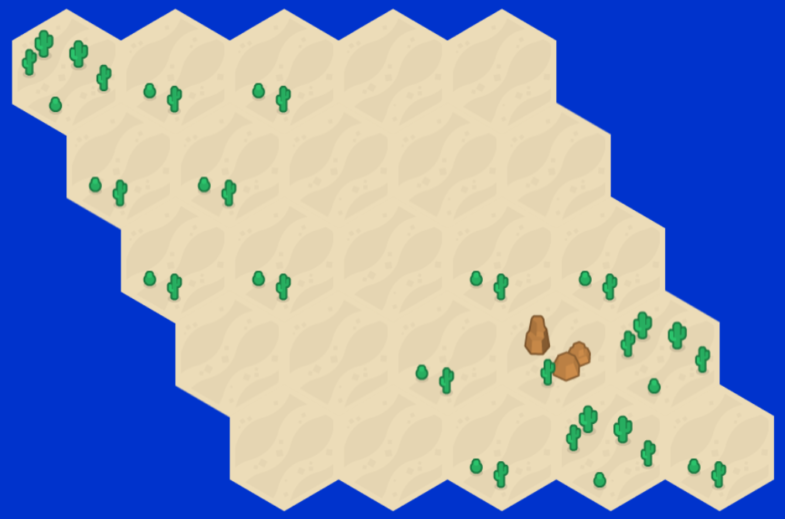
Вот что у меня получилось в итоге:

Как можно видеть, отобразилось именно такое поле как я задумывал при создании карты, выставляя циферки в двумерном массиве — лесок слева вверху и лесок с горой справа внизу.

Вертикальное поле

Для построения вертикального поля нужно просто повернуть имеющиеся тайлы на 30 градусов (+- в зависимости от особенностьей тайла), затем поменять размеры тайла и изменить формулы присвоения координат, вот итоговый код:

Код построения вертикального поля

module PhaserGame.Client {

  const MAP = [
    [{ tid: 2 }, { tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 0 }],
    [{ tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 0 }, { tid: 0 }],
    [{ tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 1 }, { tid: 1 }],
    [{ tid: 0 }, { tid: 0 }, { tid: 1 }, { tid: 3 }, { tid: 2 }],
    [{ tid: 0 }, { tid: 0 }, { tid: 1 }, { tid: 2 }, { tid: 1 }]
  ];

  const TILE_SIZE = { w: 140, h: 120 };
  const FIELD_POS = { x: 270, y: 140 };

  export class HexVertMenu extends Phaser.State {
    private mainDummy: Phaser.Sprite;
    private tnid = 0;

    private sectorWidth = 3 / 4 * TILE_SIZE.w - 2;
    private sectorHeight = TILE_SIZE.h - 1;

    private mapWidth = MAP[0].length;
    private mapHeight = MAP.length;

    create() {
      this.mainDummy = new Phaser.Sprite(this.game, 0, 0);
      this.add.existing(this.mainDummy);

      // random tile name id
      this.tnid = MyMath.randomIntInRange(0, 2);

      for (var j = 0; j < MAP.length; j++) {
        const row = MAP[j];
        for (let i = 0; i < row.length; i++) {
          const tid = row[i].tid;
          var tpos = this.getTilePosition(i, j);
          var tile = new Phaser.Sprite(this.game, tpos.x, tpos.y, 'game', DB.getTileFrameName(this.tnid, tid));
          tile.angle = 30;
          tile.anchor.set(0.5);
          this.mainDummy.addChild(tile);
        }
      }
    }

    private getTilePosition(col_id: number, row_id: number): Phaser.Point {
      var res = new Phaser.Point(
        FIELD_POS.x + col_id * this.sectorWidth,
        FIELD_POS.y + row_id * this.sectorHeight - (col_id % 2 > 0 ? this.sectorHeight / 2 : 0)
      );
      return res;
    }

  }
}

Теперь отступ делается по вертикали вверх на половину высоты тайла и он зависит от каждого второго столбца. Размер сектора теперь совпадает не по ширине, а по высоте.

Горизонтальное поле с постоянным сдвигом

Теперь построим поле вот такого вида:

Копируем код первого горизонтального поля и меняем формулу координаты по оси x:

private getTilePosition(col_id: number, row_id: number): Phaser.Point {
  var res = new Phaser.Point(
    FIELD_POS.x + col_id * this.sectorWidth + row_id * this.sectorWidth / 2,
    FIELD_POS.y + row_id * this.sectorHeight
  );
  return res;
}

Вместо попеременного сдвига мы прописываем постоянный сдвиг каждый ряд. Вот и всё.

Распознавание тайла под курсором

Вот с этой задачей не так всё просто как с прямоугольным полем. Для нахождения основного тайла под курсором мы будем использовать прямоугольную сетку из прямоугольников — секторов, а вся дополнительная сложность будет заключаться в углах шестиугольников, которые выходят за эти прямоугольники. Они помечены жёлтым на следующем рисунке.

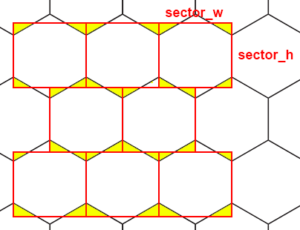
Нам нужно будет дополнительно определять, находится ли курсор в этих углах и если да, то изменять индексы текущей ячейки. И для разных видов полей алгоритмы будут отличаться.

Рассмотрим код распознавания тайла для горизонтального поля.

Модуль для горизонтального поля

module PhaserGame.Client {

  const MAP = [
    [{ tid: 2 }, { tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 0 }],
    [{ tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 0 }, { tid: 0 }],
    [{ tid: 1 }, { tid: 1 }, { tid: 0 }, { tid: 1 }, { tid: 1 }],
    [{ tid: 0 }, { tid: 0 }, { tid: 1 }, { tid: 3 }, { tid: 2 }],
    [{ tid: 0 }, { tid: 0 }, { tid: 1 }, { tid: 2 }, { tid: 1 }]
  ];

  const TILE_SIZE = { w: 120, h: 138 };
  const FIELD_POS = { x: 250, y: 100 };

  export class HexHorMenu extends Phaser.State {
    private mainDummy: Phaser.Sprite;
    private btnBack: Phaser.Button;
    private tnid = 0;
    private glow: Phaser.Sprite;

    private sectorWidth = TILE_SIZE.w;
    private sectorHeight = TILE_SIZE.h / 4 * 3;

    private mapWidth = MAP[0].length;
    private mapHeight = MAP.length;

    create() {
      this.mainDummy = new Phaser.Sprite(this.game, 0, 0);
      this.add.existing(this.mainDummy);

      // random tile name id
      this.tnid = MyMath.randomIntInRange(0, 2);

      for (var j = 0; j < MAP.length; j++) {
        const row = MAP[j];
        for (let i = 0; i < row.length; i++) {
          const tid = row[i].tid;
          var tpos = this.getTilePosition(i, j);
          var tile = new Phaser.Sprite(this.game, tpos.x, tpos.y, 'game', DB.getTileFrameName(this.tnid, tid));
          tile.anchor.set(0.5);
          this.mainDummy.addChild(tile);
        }
      }

      this.glow = new Phaser.Sprite(this.game, 0, 0, 'game', 'glow');
      this.glow.alpha = 0;
      this.glow.anchor.set(0.5);
      this.mainDummy.addChild(this.glow);

      this.btnBack = new Phaser.Button(this.game, 60, 640, 'game', this.onBackClick, this, 'Button_023', 'Button_023');
      this.btnBack.anchor.set(0.5);
      this.btnBack.scale.set(0.7);
      this.mainDummy.addChild(this.btnBack);
    }

    private onBackClick() {
      this.game.state.start(States.MAINMENU, true, false);
    }

    private getTilePosition(col_id: number, row_id: number): Phaser.Point {
      var res = new Phaser.Point(
        FIELD_POS.x + col_id * this.sectorWidth + (row_id % 2 > 0 ? this.sectorWidth / 2 : 0),
        FIELD_POS.y + row_id * this.sectorHeight
      );
      return res;
    }

    private checkTile() {
      // позиция курсора на поле, с началом координат в левом верхнем углу тайлов
      var mfpos_x = this.game.input.worldX - FIELD_POS.x + this.sectorWidth / 2;
      var mfpos_y = this.game.input.worldY - FIELD_POS.y + this.sectorHeight / 2;

      // ориентировочные координаты клетки в массиве
      var celly = Math.floor(mfpos_y / this.sectorHeight);
      if (Math.abs(celly) % 2 != 0) mfpos_x -= this.sectorWidth / 2;
      var cellx = Math.floor(mfpos_x / this.sectorWidth);

      // значения от 0 до this.sectorWidth
      var deltaX = mfpos_x % this.sectorWidth;
      if (deltaX < 0) deltaX += this.sectorWidth;
      // 0 - this.sectorHeight
      var deltaY = mfpos_y % this.sectorHeight;
      if (deltaY < 0) deltaY += this.sectorHeight;

      var tan = (TILE_SIZE.h / 4) / (TILE_SIZE.w / 2);

      var w1 = 0;
      var h1 = 0;
      if (deltaX > this.sectorWidth / 4 * 3) {
        // правый уголок
        w1 = deltaX - this.sectorWidth / 4 * 3;
        if (deltaY < this.sectorHeight / 2) {
          // верхний уголок
          h1 = deltaY;
          if (h1 / w1 < tan) {
            celly--;
            // если новый ряд нечётный, то + ещё сдвигаемся по x
            if (celly % 2 == 0) cellx++;
          }
        }
        else {
          //  нижний уголок
          h1 = this.sectorHeight - deltaY;
          if (h1 / w1 < tan) {
            celly++;
            if (celly % 2 == 0) cellx++;
          }
        }
      }
      else if (deltaX < this.sectorWidth / 4) {
        // левый уголок
        w1 = this.sectorWidth / 4 - deltaX;
        if (deltaY < this.sectorHeight / 2) {
          // верхний уголок
          h1 = deltaY;
          if (h1 / w1 < tan) {
            celly--;
            if (celly % 2 != 0) cellx--;
          }
        }
        else {
          // нижний уголок
          h1 = this.sectorHeight - deltaY;
          if (h1 / w1 < tan) {
            celly++;
            if (celly % 2 != 0) cellx--;
          }
        }
      }

      if (cellx < 0 || cellx > this.mapWidth - 1) return;
      if (celly < 0 || celly > this.mapHeight - 1) return;

      this.placeMarker(cellx, celly);
    }

    private placeMarker(cellx, celly) {
      var tpos = this.getTilePosition(cellx, celly);
      this.glow.position.set(tpos.x, tpos.y);
      this.glow.alpha = 1;
      this.glow.visible = true;
    }

    update() {
      var dt = this.game.time.elapsed * 0.001;
      this.checkTile();
    }

  }

}

Я добавил функцию checkTile() в которой и происходит вся магия. Суть такова, что если курсор находится в области угла, то находим относительные координаты точки в этом уголке и сравниваем отношение высоты к ширине (что является тангенсом угла) с заведомо заданным отношением (tan) и если оно меньше, то значит точка находится вне текущего тайла, следовательно меняем индексы текущей ячейки.

С этим рисунком должно быть понятнее:

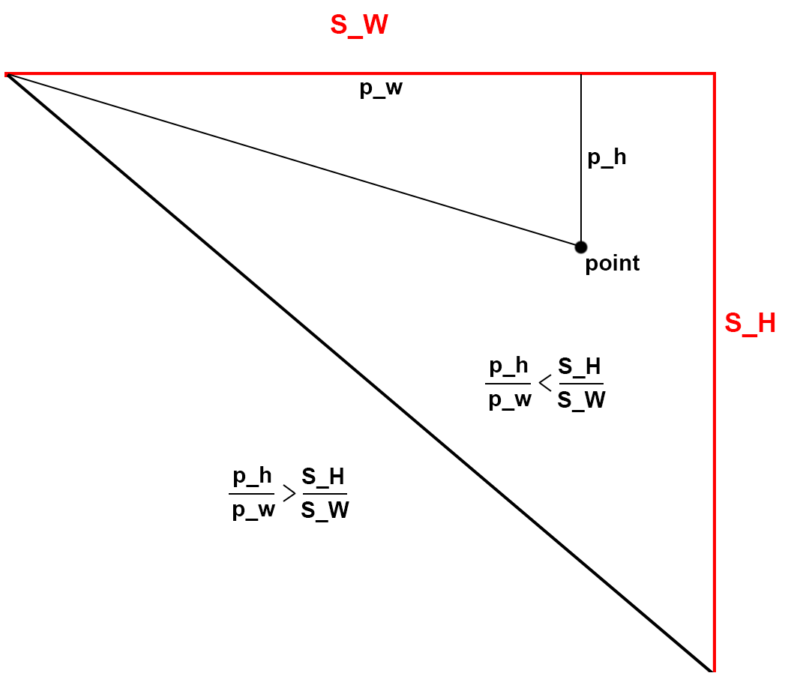
Аналогичным образом делаем для вертикального поля, а для горизонтального со сдвигом будет другая логика смещения индексов тайла.

Результат

Ну и конечно вот что получилось в итоге:

<br /> Ваш браузер не поддерживает iframe!<br />

Надеюсь эта статья поможет вам с построение вашего гексагонального поля для вашей игры, все исходники вы можете посмотреть и скачать на гитхабе по этой ссылочке.

Если есть вопросы — пишите их в комментариях.

В следующих статьях из этой серии я планирую представить алгоритмы поиска пути на гексагональном поле.

Cyber Code

Программирование, GameDev

Гексагональное поле