Дано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты.
Что нужно узнать: нужно установить принадлежность точки треугольнику.
В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику.
Метод сравнения площадей
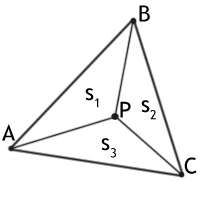
В данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно.
Затем находится площадь самого треугольника ABC.
Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность.
Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий.
Простейшая реализация алгоритма:
// проверка принадлежности точки треугольнику формулами Герона
function IsPointIn_Geron(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean;
// funcs
// площадь треугольника по точкам
function Square(aAx, aAy, aBx, aBy, aCx, aCy: single): single;
begin
Result := abs(aBx*aCy - aCx*aBy - aAx*aCy + aCx*aAy + aAx*aBy - aBx*aAy);
end;
var
s : single;
begin
s := Square(aPx, aPy, aAx, aAy, aBx, aBy) + Square(aPx, aPy, aBx, aBy, aCx, aCy) +
Square(aPx, aPy, aCx, aCy, aAx, aAy);
Result := abs(Square(aAx, aAy, aBx, aBy, aCx, aCy) - s) <= 0.01{погрешность};
end;
Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить.
Метод относительности
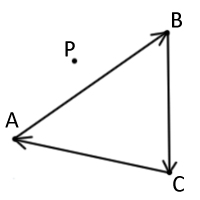
Данный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.
На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику.
Реализация алгоритма:
// проверка прин. точки треуг. методом относительности положения
function IsPointIn_Relat(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean;
// funcs
function Q(ax, ay, bx, by, atx, aty: single): single;
begin
Result := atx * (by - ay) + aty * (ax - bx) + ay * bx - ax * by;
end;
var
q1, q2, q3 : single;
begin
// выбираем определённую ориентацию по вершинам(чтоб было по порядку)
// универсальный
q1 := Q(aAx, aAy, aBx, aBy, aPx, aPy);
q2 := Q(aBx, aBy, aCx, aCy, aPx, aPy);
q3 := Q(aCx, aCy, aAx, aAy, aPx, aPy);
Result := ((q1 >= 0) and (q2 >= 0) and (q3 >= 0)) or
((q1 < 0) and (q2 < 0) and (q3 < 0));
//}
{
// для строгой ориентации по часовой
Result := (Q(ftx1, fty1, ftx2, fty2, fpx, fpy) >= 0) and
(Q(ftx2, fty2, ftx3, fty3, fpx, fpy) >= 0) and
(Q(ftx3, fty3, ftx1, fty1, fpx, fpy) >= 0);
//}
{
// для строгой ориентации против часовой
Result := (Q(ftx1, fty1, ftx2, fty2, fpx, fpy) <= 0) and
(Q(ftx2, fty2, ftx3, fty3, fpx, fpy) <= 0) and
(Q(ftx3, fty3, ftx1, fty1, fpx, fpy) <= 0);
//}
end;
Всё относительно!
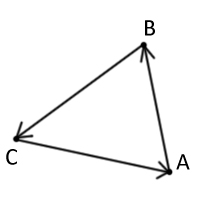
Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой.
Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику.
Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции!
Векторный метод
Третий метод который я освещаю для меня самый интересный.
Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма…
Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :]
Алгоритм такой:
1) одну вершину треугольника помещаем в координаты (0;0);
2) две стороны, выходящие из этой вершины, представляем как вектора.
Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)

Смотрим код:
function IsPIn_Vector(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean;
var
Bx, By, Cx, Cy, Px, Py : single;
m, l : single; // мю и лямбда
begin
Result := False;
// переносим треугольник точкой А в (0;0).
Bx := aBx - aAx; By := aBy - aAy;
Cx := aCx - aAx; Cy := aCy - aAy;
Px := aPx - aAx; Py := aPy - aAy;
//
m := (Px*By - Bx*Py) / (Cx*By - Bx*Cy);
if (m >= 0) and (m <= 1) then
begin
l := (Px - m*Cx) / Bx;
if (l >= 0) and ((m + l) <= 1) then
Result := True;
end;
end;
По коду можно увидеть, что находятся новые координаты точек B и C, которые одновременно являются векторами b и c (рис. 4.). А новые координаты точки P являются вектором (Px, Py). Далее идёт формула, которую я предварительно свёл к общему виду и упростил.
Кол-во основных операций получается 13(+4). Совсем не плохо :]
Метод геометрического луча
Это достаточно известный метод, особенно когда определяется принадлежность точки многоугольникам. Часто данный метод называют «трассировка луча», хотя это не совсем правильно, т.к. трассировка луча — это расчёт хода световых лучей в 3D сцене.
Суть в том, что из данной точки пускается луч по какой-либо оси в каком-либо направлении.
Затем проверяются пересечения со сторонами многоугольника и ведётся подсчёт пересечений.
Таким образом если кол-во пересечений чётное, то значит точка лежит вне многоугольника, если же кол-во НЕчётное, то значит точка лежит внутри.
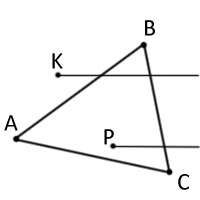
На рисунке 5 изображены две подопытные точки P и K, у луча из точки P одно пересечение со сторонами треугольника, таким образом точка P принадлежит фигуре, а точке K не повезло — у неё два пересечения.
Реализация алгоритма:
function IsPIn_RayCast(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean;
// funcs
// p1 - начало 1ого отрезка, p2 - конец 1ого отрезка, p3 - начало 2ого отрезка, p4 - конец 2ого отрезка
function peresechenie(p1, p2, p3, p4: TPoint): boolean;
var
zn, ua, ub : single;
begin // 25 операций
zn := (p4.y - p3.y) * (p2.x - p1.x) - (p4.x - p3.x) * (p2.y - p1.y);
ua := ((p4.x-p3.x)*(p1.y-p3.y) - (p4.y-p3.y)*(p1.x-p3.x)) / zn;
ub := ((p2.x-p1.x)*(p1.y-p3.y) - (p2.y-p1.y)*(p1.x-p3.x)) / zn;
// если 'ua' и 'ub' принадлежат [0,1] то отрезки пересекаются
Result := (ua >= 0) and (ua <= 1) and (ub >= 0) and (ub <= 1);
end;
var
cros_cnt : integer;
s1, s2 : single; // коэф.
begin
cros_cnt := 0; // кол-во пересечений граней (лучом из точки)
// луч пускаем по оси X вправо
// 1-я сторона треугла
s2 := (aPy - aAy) / (aBy - aAy);
s1 := aAx - aPx + s2 * (aBx - aAx);
if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then
inc(cros_cnt);
// 2-я сторона треугла
s2 := (aPy - aBy) / (aCy - aBy);
s1 := aBx - aPx + s2 * (aCx - aBx);
if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then
inc(cros_cnt);
// 3-я сторона треугла
if cros_cnt < 2 then
begin
s2 := (aPy - aCy) / (aAy - aCy);
s1 := aCx - aPx + s2 * (aAx - aCx);
if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then
inc(cros_cnt);
end;
Result := cros_cnt = 1;
end;
Вроде нормально упростил(для треугольника имею ввиду), но что-то мне кажется, что может быть и по круче…
А так, получается примерно 30 операций.
Сравнение скоростей
Ну вот мы и подошли к самому интересному! Кто быстрее и сильнее!? :]
Я провёл тест со следующими параметрами(хотя всё зависит от процессора):
- кол-во повторений алгоритма за 1 имитацию = 4 миллиона.
- кол-во имитаций для каждого алгоритма = 1000.
Таблица результатов:
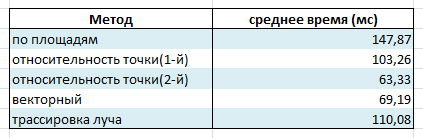
Ну что сказать, векторный метод хорош)
С ним конечно соперничает второй способ относительности точки, но главное отличие в том, что для отн. точки необходима строгая ориентация сторон треугольника, а для векторного это не важно, поэтому он круче)
Так же можно скачать написанную в ходе экспериментов программу: prin_tochki_proga. Программа реализована на Delphi 2007.